[프로그래밍언어개론]의 목적은 프로그래밍 언어를 구성하는 구문(Syntax)과 의미(Sematics)를 이해하여 다양한 프로그래밍 언어를 빠르고 정확하게 습득할 수 있는 능력을 섭렵하는 것이다. 오늘은 프로그래밍 언어가 입력 문자열을 어떻게 인식하는 지에 대한 이야기이다.
프로그래밍 언어는 알파벳 문자열로 구성된 문자열 집합이다. 그러나 알파벳 문자열 중에는 "프로그래밍 언어"가 아닌 문자열도 분명히 존재한다. 즉, 프로그래밍 언어는 알파벳 문자열로 구성된 문자열 집합 중에 "특정 문법"에 부합하는 문자열을 의미한다. "입력으로 들어오는 문자열이 "특정 문법"에 부합하는 알파벳 문자열 집합인가?"를 판별하는 역할은 구문분석기(Syntax analyzer 또는 Parser)가 하게 된다.
오늘은 입력 문자열이 특정 language에 포함되는가를 어떻게 확인하는지와 그 language를 정의하는 여러가지 expression에 대해 알아볼 예정이다.
📌Syntax and Parsing
➤ Regular language & Regularexpression
Chomsky hierarchy

Chomsky hierarchy는 언어의 표현력에 따라 계층으로 나타낸 것이다. 타원이 작을수록 해당 언어의 표현력이 작음을 나타낸다. 타원마다 automata가 존재하는데, 각각의 오토마타는 "이 문자열이 이 language에 포함되는가?"를 확인하는 역할을 한다. 오늘은 Regular language와 Context-Free language에 대해 간단하게 알아보자.
참고로 대부분의 프로그래밍 언어는 Context-Sensitive Language이거나 Context-Free Language에 속한다.
Regular language & Regular expression
Regular language는 기계가 인식할 수 있는 가장 간단한 형태의 language이다. 그리고 Regualr expression은 이러한 regular language를 정의하기 위한 문법을 의미한다. 주로 입력으로 주어진 문자열을 Tokenizing할 때 사용되며, token list로 만들어진 문자열은 automata에게 넘겨져서 language에 속하는 지 판별된다.

위 그림에서 "::="는 R이 오른쪽의 값으로 치환될 수 있음을 의미한다.
아래는 regular expression을 간결하게 사용하기 위한 연산자이다.

Regular expression의 연산자들 사이에는 다음과 같은 우선순위가 존재한다.
📝 Kleene closure > Concatenation > Union
🔍 𝑎𝑏 | 𝑐 = (𝑎𝑏) | 𝑐 = {𝑎𝑏, 𝑐}
🔍 𝑎𝑏 ∗ = 𝑎(𝑏 ∗ ) = {𝑎, 𝑎𝑏, 𝑎𝑏𝑏, 𝑎𝑏𝑏𝑏, …}
🔍 𝑎 | 𝑏 ∗ = 𝑎 | (𝑏 ∗ ) = {𝑎, 𝜀, 𝑏, 𝑏𝑏, 𝑏𝑏𝑏, …}
Regular expression을 활용하여 간단한 email address language를 정의해보자. 보통 대부분의 email은 다음과 같은 형태를 갖는다.
[문자열]@[문자열].[문자열]
이를 regular expression으로 나타내면 아래와 같다.

그러나 해당 문법은 약한 표현력을 가진다. "pi@cnu.ac.kr" 이라는 문자열을 L(email)의 언어로 인식하지 않는다. 이를 보완하려면, 뒤에 ".[문자열]"이 더 나올 수 있음을 표현해야 한다. 아래 표현식을 보자.

아직도 문제가 있다. "pi@cnu.ac.kr" 이라는 문자열은 이제 L(email)의 언어로 인식하지만, "@" 뒤에 "."이 4개 이상 올 때는 인식할 수가 없다. 예를 들어 "pi@o.cnu.ac.kr" 은 인식할 수 없다. 이를 보완하려면 "@" 뒤 ".[문자열]"의 개수에 제한을 두면 안된다. 아래와 같이 마지막 expression인 (.[a-z][a-z]*)에 kleene closure를 사용하면 ".[문자열]"의 제한을 없앨 수 있다.
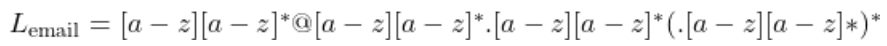
Finite (state) automata
regular expression이 regular language를 정의하기 위한 "문법"이였다면, Finite state automata는 주어진 문자열 s가 regular language에 속하는 지 판별하는 "추상 기계"이다.
Finite state automata는 입력으로 들어온 문자열에 대해서 "상태(state)"를 변경하게 되는데, 이 상태에 따라서 regular language에 속하는 지를 판별한다. Finite state automat를 기호로 표현하면 다음과 같다.

"Q"는 해당 automata가 가질 수 있는 모든 상태를 나타낸다. 그리고 "전이함수"는 입력 알파벳에 대하여 기계의 상태를 어떻게 변화할 지를 정의한 함수이다. 이전 목차에서 예시로 들었던 L(email) language에 대해 automata를 정의하면 다음과 같다.

📝 "[문자열1]@[문자열2].[문자열3](.[문자열4]))"에 대한 동작
입력 문자열을 모두 순회했을 때 기계의 상태가 q5이거나 q7이면 정상적으로 종료한다.
🔍 ------------------------------------------
처음 기계의 상태는 q0로 시작한다. 이때 "입력 문자열의 첫 번째 문자 = 소문자 알파벳"이면 q1으로 상태를 변경한다. 그리고 q1 상태에서 "다음 문자 = 소문자 알파벳"이면 "@"가 나올 때까지 q1 상태 그대로 유지한다. q1 상태에서 "@"가 나오면 q2 상태로 변경한다.
▶ "[문자열1]@" 까지에 대한 상태 변화이다.
🔍 ------------------------------------------
q2 상태에서 "다음 문자열의 첫 번째 문자 = 소문자 알파벳"이면 q3 상태로 변경한다. q3 상태에서 "다음 문자 = 소문자 알파벳"이면 q3 상태를 유지한다. q3 상태에서 "."가 나오면 q4 상태로 변경한다.
▶ "@[문자열2]." 까지에 대한 상태 변화이다.
🔍 ------------------------------------------
q4 상태에서 "다음 문자열의 첫 번째 문자 = 소문자 알파벳"이면 q5 상태로 변경한다. q5 상태에서 "다음 문자 = 소문자 알파벳"이면 q5 상태를 유지한다. q5 상태에서 "."가 나오면 q6 상태로 변경한다.
▶ ".[문자열3](." 까지에 대한 상태 변화이다.
🔍 ------------------------------------------
q6 상태에서 "다음 문자열의 첫 번째 문자 = 소문자 알파벳" 이면 q7 상태로 변경한다. q7 상태에서 "다음 문자 = 소문자 알파벳"이면 q7 상태를 유지한다.
▶ "(.[문자열4])" 까지에 대한 상태 변화이다.
L(email)을 아래와 같은 모형으로 나타낼 수도 있다.

Overall structure of compilers and interpreters

우리가 지금까지 알아본 Regular expression은 Regualr language에 대한 문법이다. 이는 automata에 의해 활용되어 입력으로 들어온 문자열을 잘게 잘라서 token list 형태로 만들어준다. 이 과정을 Tokenizing 혹은 Lexing 이라고 한다. 여기서 token이란, 프로그래밍 언어에서의 어휘 항목에 대한 표현을 의미한다. 예를 들어 "let x = 3 in f x"라는 문자열에 대해 "let"이라는 키워드도 하나의 어휘 항목이고 "in"이라는 키워드도 하나의 어휘 항목이다. "x"라는 변수도 어휘 항목이고 "=", "3", "f", "x" 모두 어휘 항목이다.
이렇게 입력으로 들어온 문자열에 대해서 해당 언어의 어휘 항목 즉, token list 형태로 만들어주는 것을 Tokenizing 혹은 Lexing이라고 하며 이 과정은 그림의 "Lexical Analysis"에서 이루어진다. 이 과정에서 문제가 발생하면 어휘 분석 오류(lexing error)를 보고한다.
이후 token list는 "Syntax Analysis"를 거쳐 "AST(Abstract Syntax Tree)"로 변환된다. 이 과정에서는 CFG(Context-Free Grammer, Context-Free laguage를 정의하는 문법)를 사용한다.
Regular expression으로 어휘 항목을 분석했다면, Context-Free Grammer로 어휘 항목들의 구조적인 묶음, 즉 프로그래밍 언어의 구문(문장 구조, syntax)을 정의하는 것이다.
그런데 Chomsky hierarchy에 따르면 Context-Free Language는 Regular Language보다 좋은 표현력을 가지고 있다. 그렇다면 어휘 항목을 정의하는 것도 CFG를 활용하면 되는 것 아니냐는 의문이 들 수 있다. 물론 가능은 하다. 하지만 과한 접근이며 처리 비용도 더 크기 때문에 사용하지 않는다. CFG는 Regular expression보다 표현력이 큰 만큼 비용이 크다. 어휘 항목을 정의하는 것은 간단한 일이기 때문에 굳이 CFG를 사용하여 프로그램의 무게를 늘릴 필요가 없다는 의미이다.
CFG(Context-Free Grammer)
이전 항목에서 알아보았듯이 CFG는 Syntax Analysis에서 token list를 받아 프로그래밍 언어의 구문을 정의하는 역할을 한다. CFG는 아래 3가지로 구성되어 있다.
📝 CFG 구성요소
🔍Terminal
▶기초 기호(literal)로써 치환되지 않는 기호
🔍Non-terminal
▶Production에 의해 치환되는 기호
🔍Production
▶Non-terminal을 치환하는 규칙
간단한 예시를 하나 들어보자.

A = 빈 문자열
A = (A) = ()
A = (A) = ((A)) = (())
A는 위와 같이 계~속 치환될 수 있다.
CFG의 엄밀한 정의는 다음과 같다.
📝 G = (Σ, N, P, S)
G는 S로부터 생성할 수 있는 모든 문자열을 나타내는 문법이다.
🔍 Σ: terminal의 유한집합
🔍 N: nonterminal의 유한집합
🔍 P: production의 유한집합
🔍 S: 시작 nonterminal (S ∈ N)
G를 아래와 같이 정의했다고 하자.

G의 원소는 시작 non-terminal인 E로부터 나타낼 수 있는 모든 문자열 집합이다.
G = {n, n+n, n-n, n+n+n, n+n-n, ...}
그런데 이렇게 CFG를 정의하니 너무나 길고 복잡하게 느껴진다. 이 때문에 CFG 기술을 위한 표기법이 따로 있는데 이를 BNF(Backus-Naur Form)이라고 부른다. 위 그림에서 정의했던 CFG를 아래와 같이 표기할 수 있다.

n을 0~9 사이의 숫자로 변경하여 다시 비교해보자.

BNF를 사용한 것이 사용하지 않았을 때보다 훨~씬 간결한 것을 볼 수 있다.
Derivation & Parse
📝 Derivation & Parse
🔍Derivation
▶정의한 CFG를 활용하여 시작 non-terminal로 부터 문자열을 생성하는 과정 (Parse의 반대 과정)
▶위에서 제시한 CFG에 대한 Derivation 예시
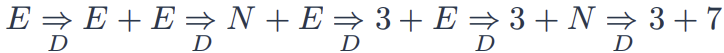
🔍Parse
▶정의한 CFG를 활용하여 입력 문자열이 문법에 부합하는 지 확인하는 과정 (Derivation의 반대 과정)
▶위에서 제시한 CFG에 대한 Parse 예시
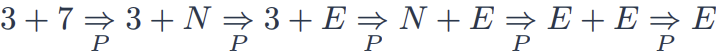
Derivation이나 Parse는 보통 tree형태로 표현하게 된다. 다음과 같은 tree를 Parse tree(or derivation tree)라고 한다. 위에서 아래로 읽으면 Derivation tree이고, 아래에서 위로 읽으면 Parse tree이므로 둘을 구분해서 나타내지는 않는다.

입력 문자열에 대한 Parsing을 진행할 때, 여러 방식으로 파싱될 수 있는 문법이 존재한다. 이러한 경우를 ambiguos(모호)하다라고 표현하는데, 하나의 문자열에 대한 여러개의 서로 다른 parse tree가 존재하므로 적절한 parsing 방법이 필요하다. 아래는 ambiguous grammer 예시이다.

이러한 경우, 두 가지 방향의 derivation 중 하나를 선택해야 한다. Left-most derivation(좌측 우선 유도)와 Right-most derivation(우측 우선 유도) 중 하나로 일관되게 표현해야 한다. Left-most derivation과 Right-most derivation은 이름 그대로 가장 왼쪽 혹은 가장 오른쪽에 있는 non-terminal부터 유도를 한다는 뜻이다. 아래는 예시이다.

derivation의 방향을 결정했다면, parsing은 다음 2가지 중 하나를 결정하게 된다. Left-most derivation을 사용할 경우 LL parsing(top-down)을 진행하게 된다. top-down 형식은 parse의 방향이 derivation과 동일하다. 위에서부터 아래로, non-terminal로부터 입력 문자열을 만들어낼 수 있는지를 확인한다. Right-most derivation을 사용할 경우 LR parsing(bottom-up)을 진행하게 된다. bottom-up형식은 아래서부터 위로, 입력 문자열로부터 non-terminal을 만들어가는 것을 의미한다.

그래서 이렇게 parsing될 수 있는 문법들을 LL grammer / language, LR grammer / language라고 부르고, 이들은 모두 Context-free grammer의 부분집합이다.
📝 LL and LR
🔍LL grammer / language
▶ LL 파싱으로 인식될 수 있는 모호하지 않은 문법 / 언어
🔍LR grammer / language
▶ LR 파싱으로 인식될 수 있는 모호하지 않은 문법 / 언어
LL(k) 또는 LR(k)도 존재하는데, 이때 k는 ambiguity(모호성)를 제거하기 위해 미리보는 토큰의 개수(lookahead)를 의미한다. 여기서 lookahead란, parsing할 때 "현재까지의 token을 어떤 non-terminal로 치환할 지 결정하기 위해, 미리 확인하는 토큰의 개수"를 의미한다.
예시로 LR(k) parsing을 진행한다고 하자. 그리고 입력 문자열이 "1 + 3 * 2" 라고 하자. 이때 lookahead가 0일 때 발생할 수 있는 문제를 생각해보자. 우선 lexing을 진행하면 token list가 만들어지고 해당 list에는 ['1'; '+'; '3'; '*'; '2']과 같은 형식으로 원소들이 존재할 것이다. 그리고 parsing을 진행하기 위해 stack을 만드는데, 이 stack은 push된 token에 대하여 termianl로 만들 수 있으면 무조건 만든다고 가정하자. 아래는 예시로 사용할 CFG이다.

lookahead가 0인 경우를 생각해보자.
📝 lookahead가 0인 경우
1) list에서 '1'이 stack에 push되면 stack의 상태는 ['1']이고 '1'이 '1' ➝ 'N' ➝ 'E' 로 치환될 것이다
▶ stack = ['E']
2) list에서 '+'가 stack에 push되면 stack의 상태는 ['E'; '+']이고 치환할 수 있는 기호가 없으므로 다음으로 넘어간다.
▶ stack = ['E'; '+']
3) list에서 '3'이 stack에 push되면 stack의 상태는 ['E'; '+'; '3']이고 '3'이 '3' ➝ 'N' ➝ 'E'로 치환될 것이다.
▶ stack = ['E'; '+'; 'E'], 이때 'E + E' ➝ 'E'로 치환될 것이다.
▶ stack = ['E']
4) list에서 '*'가 stack에 push되면 stack의 상태는 ['E'; '*']이고 치환할 수 있는 기호가 없으므로 다음으로 넘어간다.
▶ stack = ['E'; '*']
5) list에서 '5'가 stack에 push되면 stack의 상태는 ['E'; '*'; '5']이고 '5'가 '5' ➝ 'N' ➝ 'E'로 치환될 것이다.
▶ stack = ['E'; '*'; 'E'], 이때 'E * E' ➝ 'E'로 치환될 것이다.
▶ stack = ['E']
6) 모든 token에 대하여 parsing을 하였을 때, stack에 남아있는 기호가 시작 non-terminal하나만 남았으므로
parsing이 성공적으로 끝났다.
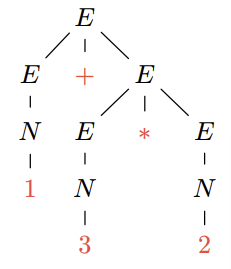
그러나 연산의 우선순위가 정해지지 않아서 문제가 발생한다. 위 과정을 parse tree로 확인해보면 다음과 같다.

따라서 lookahead가 필요하다. lookahead를 1로 설정하고 다시 생각해보자.
아까 'lookahead가 0인 경우' 의 3) 단계에서 'E + E' ➝ 'E'를 그림으로 나타내보자.

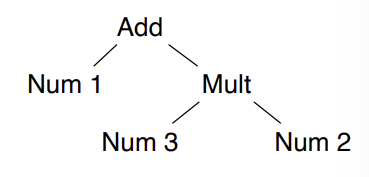
'E + E' 를 'E' 로 치환하기 전에 '*'를 lookahead로 보고 있으므로, 치환하지 않고 '*'를 stack에 먼저 push한다. 이후 '2'까지 push하고 stack의 값들을 top에서부터 치환하면 다음과 같은 parse tree를 얻을 수 있다.

'+' 연산보다 '*' 연산을 먼저 수행하므로 이번 parsing은 문제가 없는 것을 확인할 수 있다.
Abstract syntax tree(AST)

입력 문자열이 들어오면 "Lexical analysis" 단계에서 regular expression을 사용하여 문자열을 token stream으로 변경한다. token stream은 "Syntax analysis"단계에서 CFG에 따라 parsing되고 Abstract Syntax tree(AST)를 만들어낸다. 여기서 AST는 Parse tree와는 다르다.
'CS > 프로그래밍언어개론(OCaml)' 카테고리의 다른 글
| [프로그래밍언어개론] OCaml basic - 3 (0) | 2025.03.18 |
|---|---|
| [프로그래밍언어개론] OCaml basic - 2 (1) | 2025.03.17 |
| [프로그래밍언어개론] OCaml basic - 1 (1) | 2025.03.15 |

